這是個人第一次撰寫 CS 基礎知識的文章,同時也是 Rust Algorithm Club 基礎概念的首篇文章,目前 Rust Algorithm Club 尚未完工,請各位敬請期待。
(撰於 2018-05-31)
日常生活中,你會如何描述處理事情的效率?
「原來她五分鐘內可以吃掉一頭牛!」
「房間這麼小你還能擺一堆雜物?還不快收拾!」
這些描述方法,著重在處理事情的花費時間,或單位空間內的儲存量。描述演算法的效率也如此,就是「測量演算法的執行成本」,例如這個排序法花了 10 秒鐘跑完兩萬筆資料,或是這個模擬演算法很吃資源需要 32 GB 的記憶體。
然而,在不同的機器規格、環境溫濕度、程式語言、實作方式,以及有沒有放乖乖的變異影響下,相同演算法的執行成本常常不一致。為了消弭這些外部因素,讓分析演算法能夠更科學化。科學家抽絲剝繭,發明一個方法:
「統計演算法內所需操作步驟的數目。」
這是最簡單,最粗淺比較不同演算法效率的作法。
用數學表示演算法效率
「計算步驟數目」很像中小學的數學題目:某公司有三個能力相異的工程師,有的工程師一天解決一個 bug,有的工程師連續工作後效率大幅滑落。每個工程師的除蟲效率可以畫成「bug 數 - 解決 bug 所需時數」函數,橫軸為待處理的臭蟲數,縱軸為解決臭蟲所需時數,如圖一與表所示。
| 時數 | \(\log N\) | \(N\) | \(N \log N\) |
|---|---|---|---|
| \(N=5\) | 2.236 | 5 | 8.046 |
| \(N=30\) | 5.477 | 30 | 102.036 |
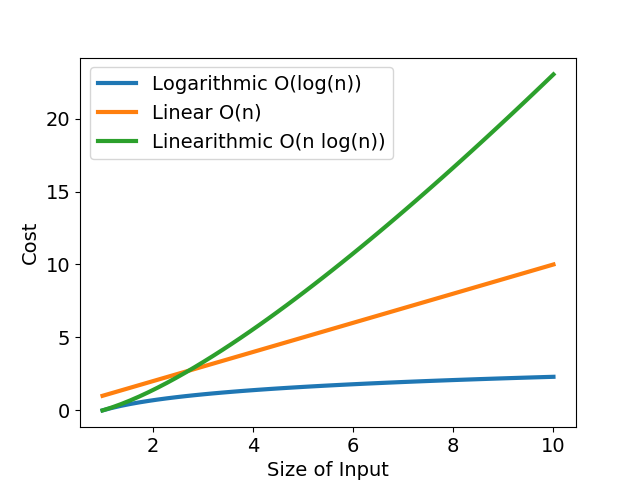
不論從圖或表,我們都可以明確看出,當 bug 數目小時,每個工程師耗時差不多;當 bug 數目成長到一定程度時,效率好與效率差的工程師差距就很明顯了。
我們把場景拉回演算法的範疇,再闡明一次。上述的除蟲效率函數關係,可以簡單視為為「輸入資料量 - 運算成本」關係之函數。例如 \(f(x)=x^2+3x+6\)。當輸入資料量增大時,成本也隨之上升,這個用來描述演算法執行成本與輸入資料量之關係的函數,我們稱之為該演算法的「複雜度」。
何謂漸進符號
了解每個演算法的時間複雜度之後,就能比較何者效率佳。但往往天不從人願,給了我們兩個演算法進行比較。
$$f(x)=\sqrt{\frac{182777}{286}}\pi x^4+5\log_{3}^{26}88x^3-e^{777^{log_2^9}}$$
$$g(x)=3x^6-2x^2$$
「天啊!這樣要怎麼分析執行效率呀!」
為了有統一的加薪標準,我們不能假定產品只會產生特定數量的臭蟲,也不能以單一天的工作表現判定員工能力,我們知道老舊系統有無限多個 bug,因此,優秀的老闆關心的是工程師長期處理「海量臭蟲」,在極限下的成長趨勢,這些成長趨勢才是衡量 KPI 的關鍵。再次強調,優秀老闆關心如何榨出是工程師的「極限成長趨勢」,而非一時半刻賣弄學識。
同樣地,有太多因素干擾影響一個演算法的複雜度,假使我們只觀察當輸入資料量 \(n\) 接近無窮大時,演算法的成長趨勢為何,就很接近所謂漸進符號(asymptotic notation)的定義。漸進符號 只關心演算法在極限下的漸進行為,不同的演算法可能使用相同的漸進符號表示。
我們比較兩個簡單函數,\(f(x) = 10x + 29\) 以及 \(g(x) = x^2 + 1\)。從圖二可以看出一開始 \(g(x)\) 的執行時間比 \(f(x)\) 多了不少,但隨著輸入資料量 \(n\) 增多,\(g(x)\) 的執行時間成長愈來愈快速,最後遠遠大於 \(f(x)\)。
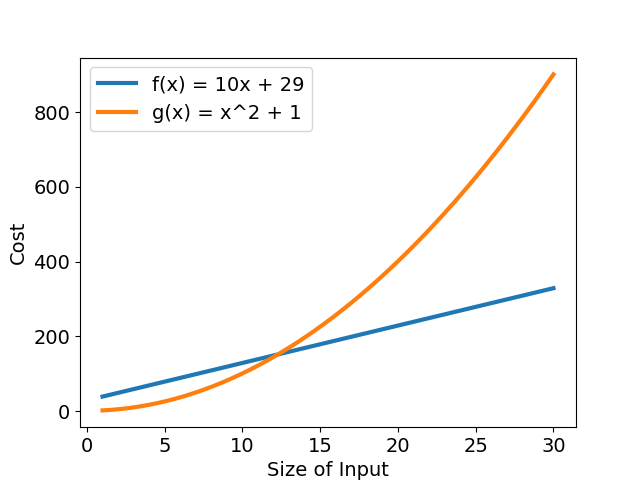
若以 \(an^2 + bn + c\) 表示複雜度,就是當存在一個 \(a > 0\) 時,一定會有 \(n\) 符合 \(an^2 > bn + c\),這個差距隨著 \(n\) 越大越明顯,這是因為首項(leading term),也就是帶有最高指數的那一項,隨著 輸入大小改變,執行時間變化幅度較大。因此,可捨去複雜度函數中其他較不重要的次項與常數,留下最大次項,「透過簡單的函數來表述函數接近極限的行為」,讓複雜度函數更易理解,這就是「漸進符號」的概念。
這裡介紹常見的幾種漸進符號:
\(O\):Big O
當我們談論演算法複雜度時,通常關心的是演算法「最糟糕的情況下」,「最多」需要執行多久。Big O 就是描述演算法複雜度上界的漸進符號,當一個演算法「實際」的複雜度(或執行成本對輸入資料量函數)為 \(f(n)\) 時,欲以 Big O 描述其複雜度上界時,必須滿足以下定義:
$$f(n) = O(g(n)) \colon {\exists k>0\ \exists n_0\ \forall n>n_0\ |f(n)| \leq k \cdot g(n)}$$
假設有一演算法實際複雜度為 \(f(n) = 3n + 4\),有一組 \(k = 4;\ g(n) = n;\ n_0 = 4\) 滿足
$$\forall n > 4,\ 0 \leq f(n) = 3n + 4 \leq 4n$$
意思是「\(f(n)\) 的複雜度上界成長趨勢最終不會超過 \(g(n) = 4n\) 」,再代入 \(O(g(n))\),可得演算法最差複雜度為 \(f(n) = O(n)\),也就是「該演算法的成長趨勢不會比 \(g(n)\) 來得快」(見圖三)。
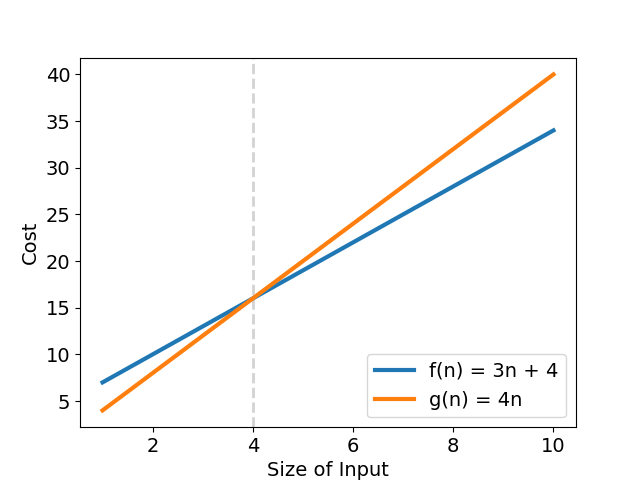
再多看一個例子,若 \(f(n) = 4n^2 + n\) 有一組 \(k = 5;\ g(n) = n^2;\ n_0 = 5\) 滿足
$$\forall n > 5,\ 0 \leq f(n) = 4n^2 + n \leq 5n^2$$
則此函數的複雜度為 \(f(n) = O(n^2)\)。
注意:也寫作 \(f(n) \in O(g(n))\),因為實際上 \(O(g(n))\) 是所以可描述演算法成長趨勢,並滿足上述條件的函數之「集合」。
\(\Omega\):Big Omega
相較於 Big O 描述演算法成長趨勢的上界,Big Omega 則是對應成長趨勢的「下界」,定義如下:
$$f(n) = \Omega(g(n)) \colon {\exists k>0\ \exists n_0\ \forall n>n_0\ |f(n)| \geq k \cdot g(n)}$$
以 \(f(n) = 3n + 4\) 為例,有一組 \(k = 2;\ g(n) = n;\ n_0 = 0\) 滿足上式,因此這個演算法在輸入資料夠大時,「至少」會達到 \(\Omega(n)\) 的複雜度,也就是「該演算法的成長趨勢不會比 \(g(n)\) 來得慢」。
\(\Theta\):Big Theta
Big Theta 則是 Big O 與 Big Omega 兩個漸進上下界所夾出的範圍,表示該演算法在輸入資料夠大時,最終的複雜度會成長到這個範圍中。其定義如下:
$$f(n) = \Theta(g(n)) \colon {\exists k_1>0\ \exists k_2>0\ \exists n_0\ \forall n>n_0\ k_1 \cdot g(n) \leq |f(n)| \leq k_2 \cdot g(n)}$$
繼續以 \(f(n) = 3n + 4\) 為例,同樣有一組 \(k_1 = 1;\ k_2 = 5;\ g(n) = n;\ n_0 = 2\),滿足
$$\forall n \geq 2,\ n \leq f(n) = 3n + 4 \leq 5n$$
可得知,\(f(n) = 3n + 4 \in \Theta(n)\),表示「該演算法的成長趨勢與 \(g(n) = n\) 相同」(見圖四)。
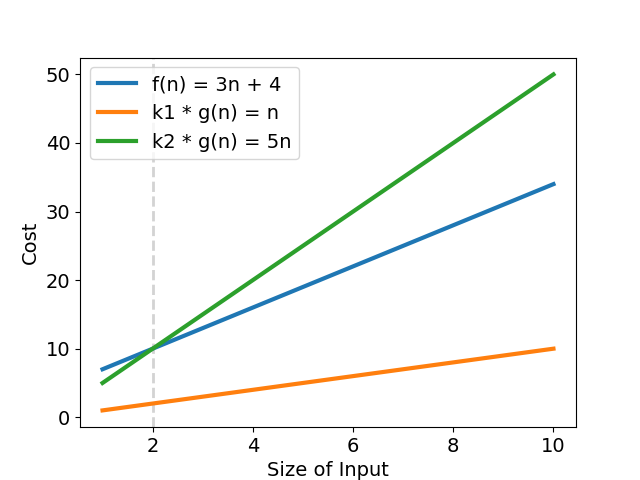
常見的複雜度
看完了讓人昏昏欲睡的數學定義,現在來認識一些常見的複雜度,從最快最有效率,到最慢最拖台錢的通通一起認識。
- \(O(1)\):常數時間,演算法執行時間與資料量毫無瓜葛。例如讀取 array 首個元素。
- \(O(\log n)\):執行時間隨資料量呈對數比例成長。常見的例子是二元搜索(Binary search)。
- \(O(n)\):執行時間隨資料量呈線性成長,例如在無序的 array 中尋找特定值。
- \(O(n \log n)\):執行時間隨資料量呈線性對數成長,常見的合併排序(Mergesort)的複雜度即如斯。
- \(O(n^2)\):執行時間隨資料量呈平方成長,例如一些效率不彰的排序法如氣泡排序(Bubble sort)。
- \(O(n^3)\):執行時間隨資料量呈立方成長,常見例子為 naïve 實作的矩陣乘法。
- \(O(c^n)\):執行時間隨資料量呈指數成長。
- \(O(n!)\):執行時間隨資料量呈階乘成長,大部分情況下,這是非常差勁的複雜度。
若想一窺各種常見演算法的複雜度,可以參考這個最全面的 Big-O Cheat Sheet,圖表非常精美直觀!
再次強調,漸進符號也可以代表其他執行成本如記憶體空間,並不一定代表執行時間。
其他的漸進符號還有 little-o、little-omega 等等,有興趣的朋友可以參考文末的資料。
你可能不適合漸進符號
善用漸進符號,可以讓原本複雜艱澀的實際複雜度,簡化至人類容易理解的簡單數學符號,也讓分析演算法效率更為客觀。但實際上,漸進符號省略了常數項與低次項,僅保留最高次項,這種「漸進行為下」的效能表現,在真實世界中,若輸入資料量不夠大,實際複雜度的低次項係數又比高次項大上許多,很可能這個演算法實際上根本沒辦法使用。
另外,漸進符號僅考慮最差與最佳複雜度,沒有考慮到平均複雜度。舉例來說,Quicksort 最差複雜度為 \(O(n^2)\),乍看之下不是很理想,但這種情況非常稀少;其平均複雜度落在 \(O(n \log n)\),且其係數相對較低,額外開銷少,自然成為最熱門的排序法之一。
還有,漸進符號也沒有考慮到不同語言、平台的基礎操作開銷,例如實作排序法時,有些語言「比較」兩個元素的開銷比「置換」來得大,實作上就需要盡量減少置換元素。同樣的,CPU 快取也非常容易忽略,一些快速的搜尋法很可能因為不是線性搜尋,沒辦法充分利用 CPU cache,效能不一定理想。
總之,漸進符號只能告訴你「當輸入資料量夠大時,演算法的複雜度表現如何」,並不總是適用每個情境,端看你怎麼使用他。